Education

A normal distribution is a probability distribution that is symmetric about the mean, with most of the data points clustered around the mean and fewer data points further away from the mean. The normal distribution is also known as the Gaussian distribution.

How to determine a normal distribution?

There are a few ways to determine if a distribution is normal. One way is to look at the shape of the distribution. A normal distribution will have a bell-shaped curve, with the highest point of the curve at the mean. Another way to determine a normal distribution is to calculate the skewness and kurtosis of the distribution. Skewness measures the asymmetry of the distribution, and kurtosis measures the peakedness of the distribution. A normal distribution will have a skewness of 0 and a kurtosis of 3.

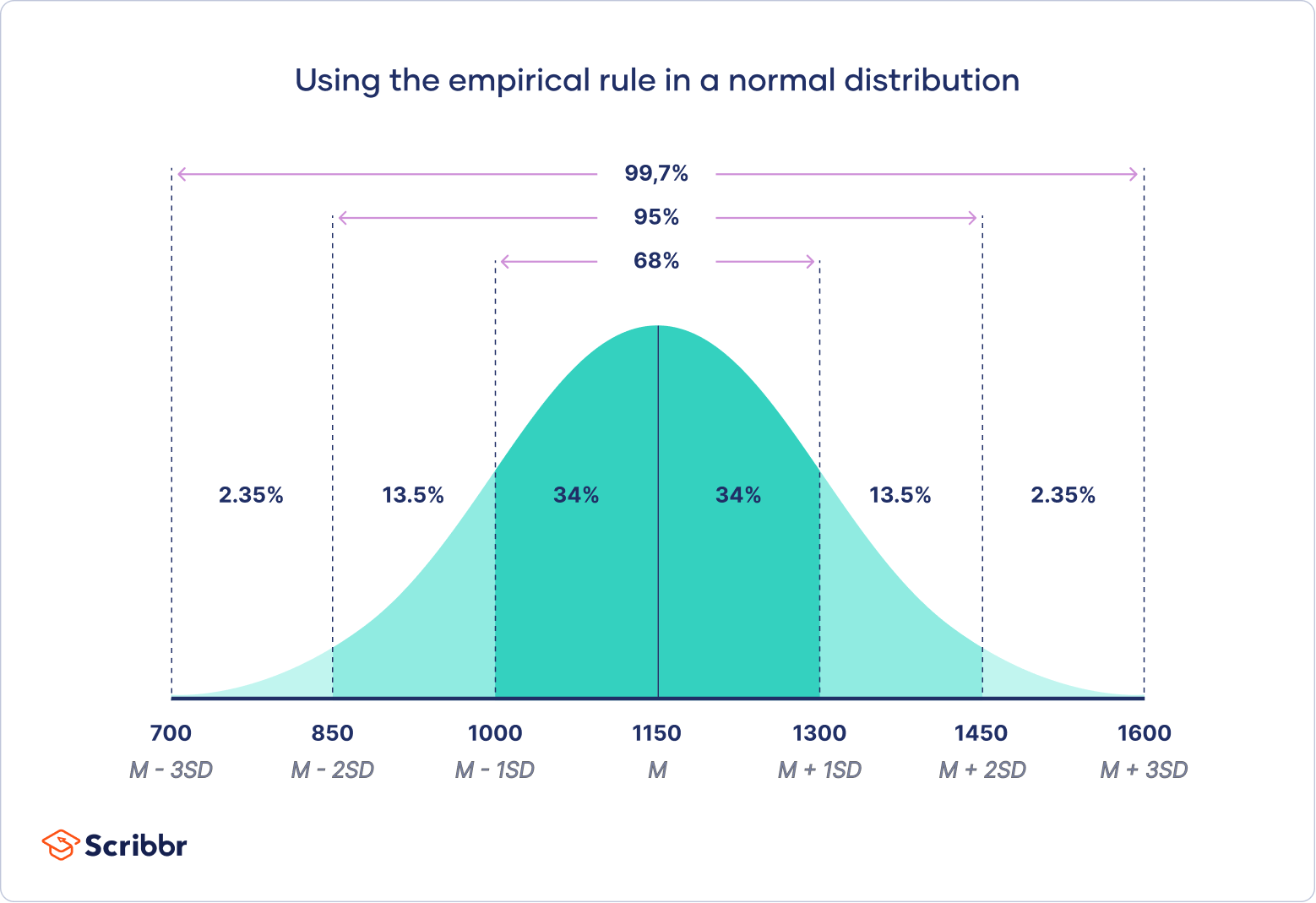
Features of a normal distribution

The normal distribution has a few key features:

• The mean, median, and mode are all equal.
• The distribution is symmetrical about the mean.
• The tails of the distribution are asymptotic to the x-axis. This means that the distribution approaches zero as the x-axis approaches positive or negative infinity.
• 68% of the data points fall within 1 standard deviation of the mean.
• 95% of the data points fall within 2 standard deviations of the mean.
• 99.7% of the data points fall within 3 standard deviations of the mean.

Standard deviation

The standard deviation is a measure of how spread out the data is in a normal distribution. The larger the standard deviation, the more spread out the data is. The smaller the standard deviation, the more tightly clustered the data is around the mean.

Z-index

The z-index is a measure of how far a data point is from the mean in terms of standard deviations. A z-score of 0 means that the data point is at the mean. A z-score of 1 means that the data point is one standard deviation above the mean. A z-score of -1 means that the data point is one standard deviation below the mean.

How to calculate the z-index

The z-index is calculated using the following formula:
z = (x - μ) / σ
Where:

• z is the z-score
• x is the data point
• μ is the mean
• σ is the standard deviation

Example of how z-index is used

This is an example how the z-index in normal distribution can be used to compare two products in a business environment:

How to use z-index to compare two products in a business environment

The z-index is a statistical measure that can be used to compare two products in a business environment. It is calculated by subtracting the mean of one product from the mean of the other product and then dividing by the standard deviation of the first product.

A positive z-index indicates that the first product is performing better than the second product, while a negative z-index indicates that the second product is performing better than the first product. The z-index can be used to compare products on a variety of metrics, such as sales, customer satisfaction, and profitability.

Example

For example, let's say you are a marketing manager for a company that sells two different types of shoes. You want to know which type of shoe is performing better in terms of sales. You can calculate the z-index for each type of shoe by subtracting the mean sales of one type of shoe from the mean sales of the other type of shoe and then dividing by the standard deviation of the first type of shoe.

If the z-index for the first type of shoe is positive, then that type of shoe is performing better than the second type of shoe in terms of sales. If the z-index for the second type of shoe is positive, then that type of shoe is performing better than the first type of shoe in terms of sales.

The z-index can also be used to compare products on other metrics, such as customer satisfaction and profitability. For example, you can calculate the z-index for each type of shoe by subtracting the mean customer satisfaction score for one type of shoe from the mean customer satisfaction score for the other type of shoe and then dividing by the standard deviation of the first type of shoe.

If the z-index for the first type of shoe is positive, then that type of shoe is performing better than the second type of shoe in terms of customer satisfaction. If the z-index for the second type of shoe is positive, then that type of shoe is performing better than the first type of shoe in terms of customer satisfaction.

The z-index is a powerful tool that can be used to compare two products in a business environment. It can be used to compare products on a variety of metrics, and it can help you make informed decisions about which products to invest in and which products to discontinue.

Here are some additional considerations when using the z-index to compare two products:

• The z-index is only a relative measure of performance. It does not tell you how well either product is performing overall.
• The z-index is only accurate if the data you are using is normally distributed. If the data is not normally distributed, you may get misleading results.
• The z-index is only one factor to consider when making decisions about products. You should also consider other factors, such as the cost of the products, the target market, and the competitive landscape.

I hope this article has helped you understand normal distribution and how the z-index can be used to compare two products in a business environment.